|
CALENDÁRIOS PERPÉTUOS
Veja o calendário de qualquer ano (do ano 1 da Era Cristã ao infinito). Observamos as regras do mundo católico. Por isso, você verá que no ano de 1582, ano da transição do Calendário Juliano para o Calendário Gregoriano, inexistiram os dias 5 a 14 de outubro: Obs.: Se você confrontar esses dados com o Microsoft/Office/Excel, verá disparidade no ano de 1900. O problema é do Excel, que considera 1900 um ano bissexto, incorretamente. Qualquer tentativa de calcular datas antigas (anteriores a 1º de março de 1900), partindo do calendário do Excel, vai dar erro de 1 dia. Esse erro vem do Lotus 1-2-3 e foi propositadamente assumido pelo Excel, visando compatibilizar ambas as planilhas. A título de curiosidade, você pode visualizar calendários de 1 a 4713 A.C., digitando 0 para o ano 1, -1 para o ano 2, -2 para o ano 3 e assim sucessivamente, até -4712 para o ano 4713. O algoritmo para esse cálculo está na minha página Dias Julianos. Observe que isso se refere a calendários hipotéticos, sem valor histórico. Registros históricos confiáveis só existem a partir do século 4 da Era Cristã. O Menor Calendário Perpétuo do Mundo! Calendários de bolso, anunciados como perpétuos, eu conheço muitos, há pelo menos 50 anos. Nenhum é perpétuo. O primeiro que eu conheci abrangia apenas 28 aos. Depois conheci outros que abrangiam 40, 50 e 100 anos. Ainda hoje eles são ofertados pelo mundo. No ano de 1994 fiz-me o desafio de criar um calendário de bolso efetivamente perpétuo. No começo de 1995 eu já havia chegado à solução. No mesmo ano (3/2/1995) obtive o registro do invento no INPI - Instituto Nacional da Propriedade Industrial, sob número PI 9500471-8. No ano seguinte divulguei o invento na Internet, nesta página que mantenho até hoje. O grande diferencial, que o faz inédito no mundo, é que este calendário combina milhar/centena do ano desejado com dezena/unidade, permitindo qualquer composição de data, de janeiro do ano 1 da Era Cristã até o infinito. Observe, a título de curiosidade, que tudo se repete, no Calendário Gregoriano, a cada 4 séculos, e a cada 7 séculos no Calendário Juliano. Conheça, portanto, o menor (e único) calendário perpétuo de bolso no mundo, que abrange qualquer data da era cristã, do ano 1 ao infinito. Imprima, recorte e una os três discos com um ilhós ou um rebite. 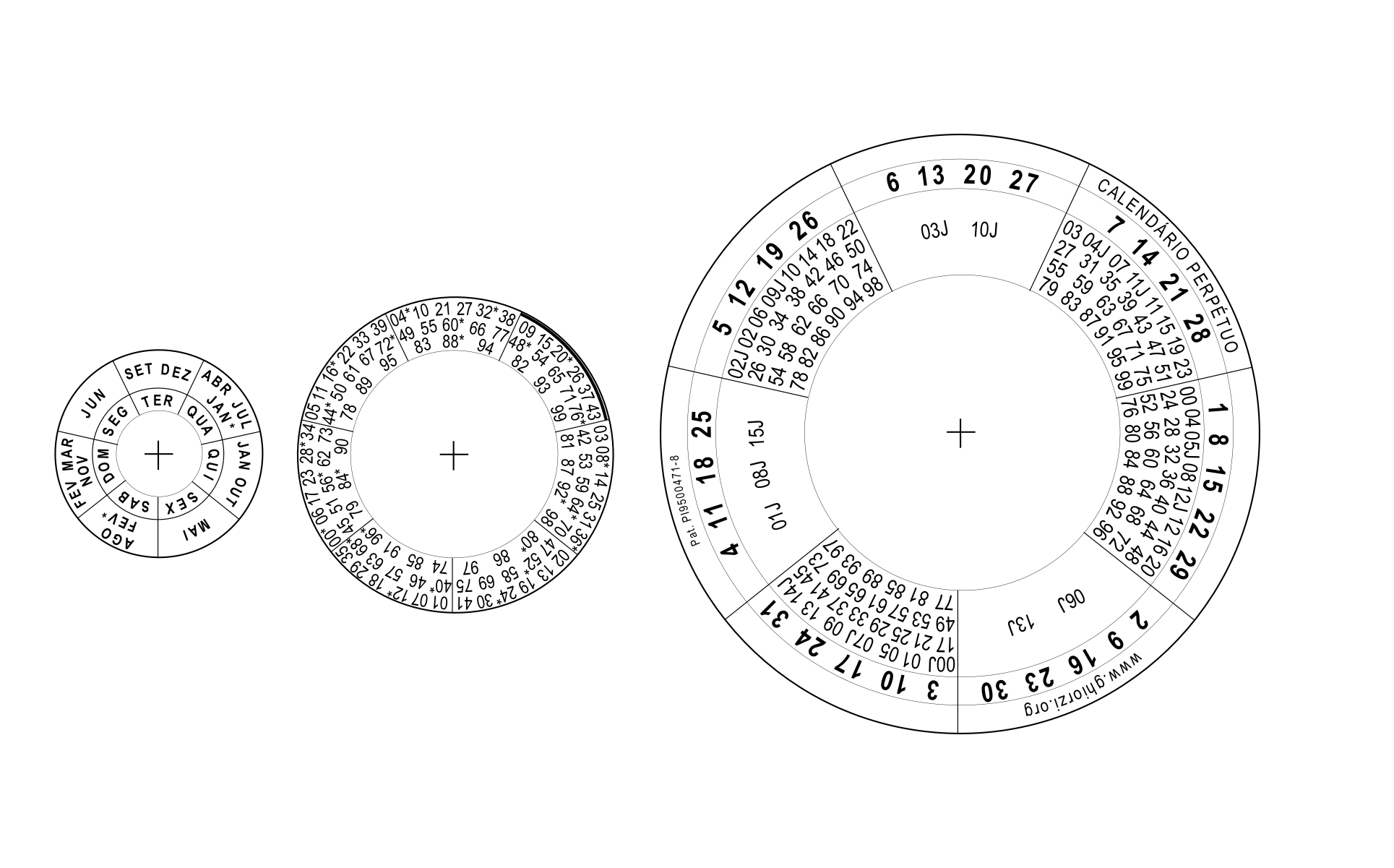 O novo artefato contém todos os milhares/centenas, de 00 a 99, constituindo o único calendário perpétuo de bolso que não tem limites. Qualquer que seja a data, do ano 1 da Era Cristã ao infinito, você pode vê-la em cinco segundos, ainda que seja, hipoteticamente, o ano de 99999999999... pois somente os 4 últimos algarismos (unidade, dezena, centena e milhar) interessam. Os algarismos a partir do 5º da direita para a esquerda são indiferentes para o cálculo. Exemplo prático: Em que dia da semana cairá a data 6 de agosto de 516763? Data: 06/08/516763 (milhar/centena=67 dezena/unidade=63) Gire o disco do meio, posicionando o arco (A) sob o segmento que contém o milhar/centena 67 (B) no disco de fora. Não mexa mais nesses dois discos. Gire o disco de dentro, posicionando o mês de AGO (C) sob o segmento que contém a dezena/unidade 63 (D) no disco do meio. Localize na parte mais externa do disco de fora o dia 6 (E) e veja que ele está sobre o dia da semana TER (F). Terça-feira, portanto. Observe que o disco mais externo e o disco mais interno exibem o inteiro calendário do mês desejado. 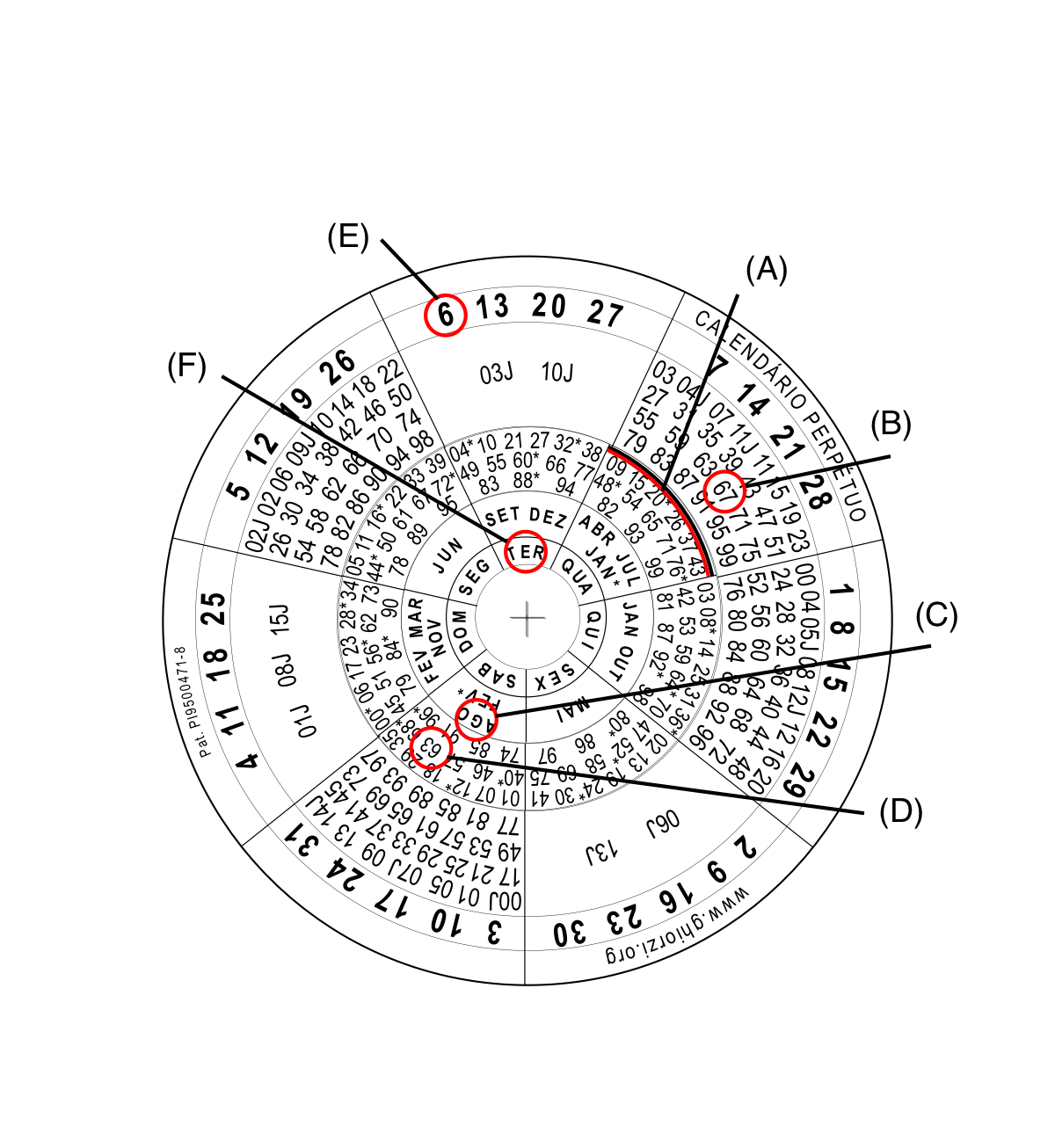
Importante: Ao trabalhar com datas do Calendário Juliano (até 4/10/1582), use excepcionalmente os milhares/centenas seguidos da letra "J". Nos países onde o Calendário Juliano invadiu o ano 1600, 1700 e assim por diante, basta incluir 16J no setor 09J, 17J no setor 10J e assim por diante. A título de curiosidade, veja outros modelos experimentais de calendários perpétuos de bolso, que vimos desenvolvendo a partir de 1995.
Um pouco de História... Mas em 8 a.C. o oitavo mês ("sextilis") teve o nome mudado para agosto, em homenagem ao então imperador César Augusto e, como o mês de julho (em homenagem a Júlio César) tinha 31 dias, resolveu-se igualar o número de dias de agosto, subtraindo 1 dia de fevereiro, que ficou com 28 ou 29 dias, e se alterou a seqüência dos meses de 31 dias (outubro e dezembro teriam 31 dias, no lugar de setembro e novembro). O mês de março - mês do auge da primavera no hemisfério norte - era efetivamente o primeiro mês do ano. Observe, a esse propósito, que SETEmbro era o sétimo mês. Só mais tarde o mês de janeiro - mês do início do mandato dos cônsules romanos - passou a ser o primeiro e não o décimo-primeiro mês do ano. Isso definiu as atuais regras dos meses com 31 dias (janeiro, março, maio, julho, agosto, outubro e dezembro), com 30 dias (abril, junho, setembro e novembro) e com 28 ou 29 dias (fevereiro). O Calendário Juliano terminou em 4 de outubro de 1582, uma quinta-feira. O Calendário Gregoriano iniciou em 15 de outubro de 1582, uma sexta-feira, suprimindo da história os dias 5 a 14 de outubro de 1582. Portugal e suas colônias adotaram a reforma Gregoriana no seu começo, mas muitas nações, incluindo a Inglaterra, fizeram-no depois. Assim, nos países de língua inglesa, os dias suprimidos foram 3 a 13 de setembro de 1752. Ao redor do mundo, nós tivemos muitas exceções. Na Bulgária, por exemplo, os dias suprimidos foram 1 a 13 de abril de 1916. A Turquia foi mais longe: suprimiu os dias 19 a 31 de dezembro de 1926.
O nome dos meses
Anos bissextos Diferentemente da crença popular, o nome "bissexto" não teve origem no fato de anos bissextos contarem 366 dias. A explicação correta é que o dia complementar seria colocado entre o sétimo e o sexto dia anteriores às "calendas de março" (isto é, entre 23 e 24 de fevereiro - mês que na época tinha 29 dias, normalmente), o que fez denominá-lo "bissexto calendas" (em outras palavras, dois "sextos dias" antes de março). Uma curiosidade: registros históricos dão conta de que o ano 4 da nossa era não foi bissexto. Teria havido um erro de interpretação, que fez contarem os anos bissextos de três em três, durante os primeiros anos de vigência do Calendário Juliano. Para corrigir isso, o imperador César Augusto teria determinado um lapso, entre 8 a.C. e 8 d.C., em que os anos múltiplos de quatro não seriam bissextos.
Ano trópico Mas, no tempo do Papa Gregório XIII, já se sabia que o número era outro. Hoje ele está definido como 365,24219271 dias [365d5h48m45,4501s] (em vez dos antigos 365,25) e diminui à razão de 0,005369 segundo por ano. Por isso o Calendário Gregoriano substituiu o Calendário Juliano, fazendo o mencionado acerto dos 10 dias e estabelecendo as mencionadas correções extraordinárias a cada 100 anos. Isso compatibilizou o nosso calendário com a Astronomia, mas persiste um erro de 25,96768 segundos por ano, o que demandaria um novo ajuste, por exemplo, suprimindo outro ano bissexto por volta de 4909, 8236, 11563 etc. (no livro "Calendário" de David Ewing Duncan). Mas isso é muito preciosismo, pois nós sequer sabemos se a Terra sobreviverá ao 3º milênio, diante da maldade e da irresponsabilidade dos seres humanos! [Por que 25,96768 e por que 4909, 8236, 11563 etc.? Porque 25,96768 é o número calculado pelos astrônomos (diferença entre o ano gregoriano 365d05h48m20s e fração e o ano trópico 365d05h48m45s e fração) e porque o dia tem 86.400 segundos, que divididos por 25,96768 resultam 3.327 anos. Partindo do pressuposto que o calendário estava astronomicamente correto no fim de 1582, o novo ajuste de 1 dia deveria ser feito por volta de 4909 (1582+3327), 8236 (4909+3327), 11563 (8236+3327) etc. Fazendo não bissextos, por exemplo, os anos de 4908, 8236, 11564 etc.]
O Calendário Ideal Todos os 13 meses teriam idêntica configuração:
 Leitores da minha página têm feito perguntas sobre particularidades do novo calendário. Tento esclarecer-lhes:
P.
---------------------------------------------------------------------------------------
Janeiro Fevereiro Março Abril Maio Junho
Antigo 01 08 15 22 29 05 12 19 26 05 12 19 26 02 09 16 23 30 07 14 21 28 04 11 18 25
Novo 01 08 15 22 01 08 15 22 01 08 15 22 01 08 15 22 01 08 15 22 01 08 15 22 01 08
01 02 03 04 05 06 07
---------------------------------------------------------------------------------------
Julho Agosto Setembro Outubro Novembro Dezembro
Antigo 02 09 16 23 30 06 13 20 27 03 10 17 24 01 08 15 22 29 05 12 19 26 03 10 17 24 31
Novo 15 22 01 08 15 22 01 08 15 22 01 08 15 22 01 08 15 22 01 08 15 22 01 08 15 22 29
07 08 09 10 11 12 13
---------------------------------------------------------------------------------------
Os dias da semana
Inglês Espanhol Italiano Francês
Domingo Sol Sunday Domingo Domenica Dimanche
Segunda Lua Monday Lunes Lunedi Lundi
Terça Marte Tuesday Martes Martedi Mardi
Quarta Mercúrio Wednesday Miércoles Mercoledi Mercredi
Quinta Júpiter Thursday Jueves Giovedi Jeudi
Sexta Vênus Friday Viernes Venerdi Vendredi
Sábado Saturno Saturday Sábado Sabato Samedi
O nome dos dias da semana
Uma observação oportuna
Cálculo mental do dia da semana Observemos que 1/1/1901 foi uma terça-feira. Consideremos 1=dom 2=seg 3=ter 4=qua 5=qui 6=sex 0=sab.
a) escolha uma data qualquer, de 1/1/1901 a 31/12/2099 Veja o exemplo prático abaixo:
a) 27/03/2013
a) 17/04/1940 *setes fora=o resto de um número dividido por sete O período escolhido acima, 1901/2099, é o período mais consultado atualmente e por isso o elegemos. Além disso, é o período com menos complicadores. Todavia, é perfeitamente possível estender a rotina de cálculo mental do dia da semana para os anos anteriores ou posteriores, desde o ano 1 da Era Cristã até o infinito, se o leitor estiver disposto a enfrentar as complicações dos anos terminados em "00" não bissextos (1700, 1800, 1900, 2100, 2200, 2300, 2500 etc.) e dos 10 dias suprimidos na transição do Calendário Juliano para o Calendário Gregoriano (5 a 14 de outubro de 1582). Damos a seguir a rotina alternativa, para funcionar do ano 1 da Era Cristã ao infinito:
Observemos que o primeiro dia da Era Cristã foi teoricamente um sábado. E novamente consideremos 1=dom, 2=seg 3=ter, 4=qua, 5=qui, 6=sex e 0=sab.
a) escolha uma data qualquer, do ano 1 ao infinito
*matematicamente queremos "diminuir 1", mas não convém trabalhar com números negativos (observe que -1 equivale a +6 em operações com setes fora)
Veja o exemplo prático abaixo:
Veja outro exemplo prático:
Veja mais um exemplo prático, com o mês de 21 dias (outubro de 1582):
Cultura inútil 00 28 56 84 OUT 01 29 57 85 ABR-JUL 02 30 58 86 SET-DEZ 03 31 59 87 JUN 04 32 60 88 FEV-AGO 05 33 61 89 MAI 06 34 62 90 JAN-OUT 07 35 63 91 ABR-JUL 08 36 64 92 JUN 09 37 65 93 FEV-MAR-NOV 10 38 66 94 AGO 11 39 67 95 MAI 12 40 68 96 JAN-ABR-JUL 13 41 69 97 SET-DEZ 14 42 70 98 JUN 15 43 71 99 FEV-MAR-NOV 16 44 72 MAI 17 45 73 JAN-OUT 18 46 74 ABR-JUL 19 47 75 SET-DEZ 20 48 76 MAR-NOV 21 49 77 AGO 22 50 78 MAI 23 51 79 JAN-OUT 24 52 80 SET-DEZ 25 53 81 JUN 26 54 82 FEV-MAR-NOV 27 55 83 AGO |
© 20/05/1996 Atualizada em 08/03/2025