DEEP BLUE X KASPAROV

O torneio Deep Blue x Kasparov, (3 a 11 maio 1997), vencido pelo computador, reacendeu as discussões em torno do futuro do xadrez. Insinua-se que a máquina vai abater o homem, inexoravelmente.

Alegam os profetas de plantão que a velocidade da máquina (200 milhões de movimentos por segundo) logo ultrapassará todas as possibilidades de reação do ser humano, cujo cérebro, dizem, estacionou nos atuais limites de cálculo conhecidos.

Façamos um cálculo simples, para sugerir calma a esses profetas do juízo final: Uma partida plausível de xadrez pode ter 40 lances, com probabilidade de 35 movimentos diferentes para cada lado, por jogada. Significa que, para resolvê-la matematicamente, teriam de ser analisados 3,35x10^123 movimentos (35^80). Para resolvê-la em 2 horas (tempo oficial para 40 lances), o computador teria de contar com uma velocidade de 4,66x10^119 movimentos por segundo (3,35x10^123÷7.200), ou seja, o número 466 seguido de 117 zeros!

Quando o computador alcançará essa velocidade? Dizem que a velocidade dos computadores tende a dobrar a cada 13 meses, como acontece na atualidade. Considerando, assim, que 466 seguido de 117 zeros equivale a 200.000.000x2^370 e que 370x13÷12=400, podemos dizer que tal velocidade só será alcançada em 400 anos!

Todavia, prevê-se que o primeiro computador comercial quântico da IBM, anunciado em 2019, poderá reduzir esse período de 13 meses para 12 horas, o que levará a alcançar essa velocidade já nos próximos 185 dias, ou seja, o resultado de 370x12÷24!! Estaremos, portanto, a poucos meses da possibilidade de solucionar o jogo de xadrez!!!

Muitos dirão que, alcançada essa velocidade, todas as partidas jogadas por duas máquinas resultarão inexorável empate. Eu não penso assim. Eu penso que as brancas sempre vencerão! Exatamente como acontece com quem inicia o Jogo dos Quinze Palitos! Pois que estará definitivamente desvendado o segredo dos lances iniciais vencedores!

É claro que estou argumentando em termos estritos de algoritmo, sem que o computador, a cada lance do oponente, recorra a bibliotecas, como fez para vencer Kasparov. Admitiria que o computador recorresse a bibliotecas no contexto da diversão, mas não no campo da competição.

Para se ter idéia da lentidão do computador, 200 milhões de movimentos por segundo não contemplam sequer a análise de 4 lances futuros para ambos os lados (nos 3 minutos médios de que se dispõe para cada lance). Só isso demandaria velocidade superior a 12,5 bilhões de movimentos por segundo! (35^8÷180).

E, algoritmo por algoritmo, o homem está mil anos à frente da máquina, porque, enquanto ela calcula um milhão de movimentos, ele descarta 10 milhões. É a diferença entre cálculo e raciocínio.

Continuo apostando no ser humano.

KASPAROV CONTRA O MUNDO

É fácil prever que Kasparov forçará "o mundo" a abandonar essa partida de xadrez antes do trigésimo lance, pois a maioria dos votantes é constituída de enxadristas medíocres. Qualquer enxadrista mediano pode vencer idêntico desafio. Com certeza Kasparov sabe que não estará enriquecendo seu currículo com essa vitória, mas procura apenas promover o esporte, no que tem o integral apoio dos amantes do xadrez. (7 jul 1999)

A Partida (Kasparov contra O Mundo - 21 jun 1999)

1. e4 c5 2. Cf3 d6 3. Bb5+ Bd7 4. Bxd7+ Dxd7 5. c4 Cc6 6. Cc3 Cf6 7. O-O g6 8. d4 cxd4 9. Cxd4 Bg7 10. Cde2 De6 11. Cd5 Dxe4 12. Cc7+ Rd7 13. Cxa8 Dxc4 14. Cb6+ axb6 15. Cc3 Ta8 16. a4 Ce4 17. Cxe4 Dxe4 18. Db3 f5 19. Bg5 Db4 20. Df7 Be5 21. h3 Txa4 22. Txa4 Dxa4 23. Dxh7 Bxb2 24. Dxg6 De4 25. Df7 Bd4 26. Db3 f4 27. Df7 Be5 28. h4 b5 29. h5 Dc4 30. Df5+ De6 31. Dxe6+ Rxe6 32. g3 fxg3 33. fxg3 b4 34. Bf4 Bd4+ 35. Rh1 b3 36. g4 Rd5 37. g5 e6 38. h6 Ce7 39. Td1 e5 40. Be3 Rc4 41. Bxd4 exd4 42. Rg2 b2 43. Rf3 Rc3 44. h7 Cg6 45. Re4 Rc2 46. Th1 d3 47. Rf5 b1=D 48. Txb1 Rxb1 49. Rxg6 d2 50. h8=D d1=D 51. Dh7 b5 52. Rf6+ Rb2 53. Dh2+ Ra1 54. Df4 b4 55. Dxb4 Df3 56. Rg7 d5 57. Dd4+ Rb1 58. g6 De4 59. Dg1+ Rb2 60. Df2+ Rc1 61. Rf6 d4 62. g7 1-0 (22 out 1999)

O Mundo - 0

Kasparov - 1

Análise do Fim do Jogo, por Kasparov

Mate em 25 lances - 62....Dc6+ 63. Rg5 Dd5+ 64. Df5 Dg2+ 65. Dg4 Dd5+ 66. Rh4! Dg8 67. Df4+ Rc2 68. Df8 Dh7+ 69. Rg5 Dh2 70. g8=D Dg3+ 71. Rf5 Df3+ 72. Re6 Db3+ 73. Rd6 Db4+ 74. Re5 De1+ 75. Rxd4 (mate em 12) Da1+ 76. Re4 Da4+ 77. Re3 Da7+ 78. Rf3 Db7+ 79. Rg3 Dc7+ 80. Df4 Dxf4+ 81. Rxf4 Rd3 82. Db3+ Rd4 83. Db5 Rc3 84. Re3 Rc2 85. Db4 Rc1 86. Rd3 Rd1 87. Dd2++

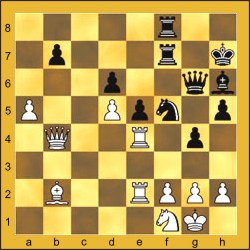
O torneio Fritz x Kasparov, (11 a 18 novembro 2003), empatado, desilude-me a respeito da honestidade dos participantes. O suspeitíssimo lance 32...Tg7?? de Kasparov, na 2ª partida (entregando o peão do rei e a partida), e o suspeitíssimo lance 14...Bd6?? de Fritz, na 3ª partida (tola tentativa de tomar a dama branca), fazem-me acreditar em um torneio com cartas marcadas. Ninguém me convence de que, no primeiro caso, Kasparov não tenha entregue deliberadamente a partida e, no segundo caso, de que não tenha havido interferência humana naquele lance absolutamente malicioso e infantil:

2ª partida - Próximo lance 32...Tg7??

3ª partida - Próximo lance 14...Bd6??

Retiro minhas apostas em Kasparov. E não aposto nesses computadores, meio-máquinas, meio-humanos. Eu não esqueço de que no torneio anterior (Deep Blue x Kasparov) o próprio Kasparov acusou a IBM de fraude e o mundo enxadrístico levantou suspeitas sobre a conduta de Kasparov. Fica a pergunta: Estivemos assistindo torneios de xadrez ou propaganda enganosa dos fabricantes do "Deep Blue" e do "Fritz"?

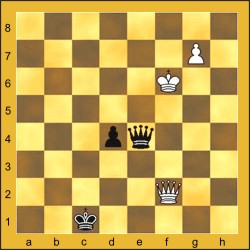
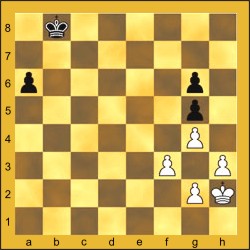
Você sabia que a menor partida completa de xadrez tem apenas 2 lances? Confira: 1. f3 e6 2. g4 Dh4++

CURIOSIDADE II

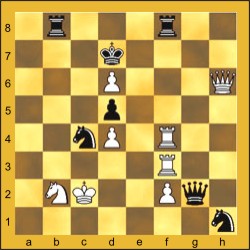
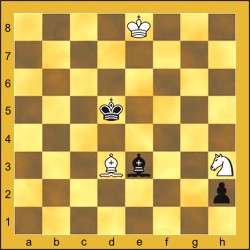
Recuperação de uma lenda contada no "Manual de Xadrez" de Idel Becker (Editora Nobel, 1948) e no livro "Lendas do Deserto" de Malba Tahan (Editora Record, 1988). Idel Becker apresentava-a como um problema de "mate em 7 lances", anunciado pelas brancas, e atribuía a história a Charles Godfrey Gimpel (1876). Malba Tahan reinventava a lenda, invertendo-a para mate anunciado pelas pretas, mas omitia o principal: os lances da partida.

Refaço a história completa, sem a pretensão de fazê-lo à altura dos geniais escritores que a inspiraram:

Conheci na célebre cidade de Damasco, já lá se vão muitos anos, um velho enxadrista cristão, chamado Ibrahim Calemah.
Era um homem baixo, calvo, de barbas brancas. Tinha o nariz deformado por uma cicatriz. Os seus olhos negros, extremamente vivos, pareciam dois pequeninos besouros do deserto que os árabes de minha tribo denominavam astemalak.
Contaram-me os damascenos que o xeque Ibrahim, por causa da sua incorrigível mania e paixão pelo jogo de xadrez, se envolvera em perigosas aventuras.
De uma feita, viu-se em séria atrapalhação com o próprio Diabo!
Com o Diabo?
Devia ser surpreendente essa aventura do cristão com o Maligno, que os árabes denominam Cheitã. Procurei conhecê-la. E um dia, finalmente, naquele pequeno café, que fica junto à porta de Santo Tomás, interroguei sobre o caso o famoso enxadrista.
Como conseguira ele enfrentar o próprio Gênio do Mal?
O velho Ibrahim, com sua enorme paciência, contou-me o seguinte:
– Nesse tempo eu não passava de um presumido enxadrista. A vaidade encastelara-se em meu coração. Tinha-me na conta de invencível. Conhecia milhares de golpes, lances secretos, contra-ataques e xeques que seriam suficientes para desnortear o adversário mais perigoso.
Uma noite, depois de ter derrotado, num violento torneio, vários campeões, um de meus amigos interpelou-me:
– Você teria coragem de bater-se contra o Emir de Hedjaz, o campeão da Arábia?
– Ora, ora, respondi em tom de menoscabo. Eu seria capaz de jogar xadrez até com o Diabo!
– Aquela minha descabida bravata, dita com seriedade e convicção, surpreendeu os meus companheiros. Um pesado e impressionante silêncio seguiu-se às minhas palavras. Um maronita, bom católico, fitou-me horrorizado e respondeu-me circunspecto:
– Não diga isso, Ibrahim! É uma afronta à nossa crença!
– Qual afronta, nem meia afronta, repliquei desabusado. Diante do tabuleiro não temo adversário algum!
– Nessa noite, entretanto, ao regressar para casa, sentia que praticara uma grave imprudência. Uma inquietação indefinível pesava em meu espírito já um pouco conturbado. Procurei dominar a sensação de temor que pouco a pouco me invadia.
– A noite estava muito escura. Poucas estrelas se avistavm no céu de Damasco. O vento, com rajadas incertas, varria as ruas desertas, uivando como um chacal faminto.
– Passei por Aab-el-Feredj, caminhei pela rua Menac e cheguei, finalmente, a nossa casa em Elebeh. Minhas irmãs, dias antes, haviam seguido para Jerusalém e eu me achava, por isso, só.
– Abri cautelosamente a porta e entrei. Acendi logo a vela e encaminhei-me para o meu quarto.
– O tabuleiro de xadrez, com as suas trinta e duas peças, achava-se justamente como eu o havia deixado.
– E como se me sentisse vagamente nervoso e sem sono, resolvi analisar uma das partidas que havia jogado, de tarde, durante o torneio. Preparei, pois, o tabuleiro e arrumei todas as peças em seus lugares.
– Nesse momento ouvi um estranho ruído. Voltei-me rápido e vi, de pé, diante de mim, um cavalheiro alto, de ombros largos, todo vestido de preto. O seu rosto era cor de bronze e seus olhos desprendiam um estranho lume.
– Quem é o senhor? Bradei, tomado de indizível espanto. Que deseja a esta hora em minha casa?
– Calma, meu amigo, respondeu o desconhecido, fitando-me nos olhos, penetrantemente. Calma, ó xeque Ibrahim! Em poucas palavras explicarei o motivo desta minha inesperada visita. Ouvi hoje o teu insensato desafio. A tua petulância irritou-me. E aqui estou para medir a tua tão celebrada força de enxadrista.
– Só então percebi, trêmulo de pavor, que tinha diante de mim o Diabo – aquele inimigo que os árabes chamam Cheitã, o Infernal.
– Procurei dominar-me e balbuciei: Não me bato com o Demo!
– Mudarás de idéia, meu caro! Ameaçou Satã acompanhando as suas palavras de uma risadinha estridente, metálica, desagradável.
– O desafio foi teu. E agora estás obrigado a aceitar-me como adversário.
– E depois de uma ligeira pausa, prosseguiu com severíssima catadura:
– Vamos jogar uma única partida. Se venceres, receberás, como prêmio, esta bolsa com cem libras. Se perderes, eu levarei tua alma!
– Já mais calmo, enchi-me de coragem e respondi: Aceito a sua proposta. Vamos ao jogo, Sr. Diabo!
– Uma condição ainda, advertiu num tom muito grave o temível Cheitã: Durante a nossa partida, não esboçarás gestos nem dirás palavras que sejam incompatíveis com a minha presença. Prometes?
– Assim o prometo, confirmei com segurança.
– Sentamo-nos em silêncio diante do tabuleiro. O Diabo escolheu as peças pretas. Eu sabia que a minha situação era desesperadora: Se eu vencesse, o Diabo, enfurecido, logo esqueceria seu compromisso e me levaria à perdição. Se eu perdesse, como escapar das garras do Infernal?
– Eu teria de agir com a astúcia do mestre dos mestres do xadrez!
– Aproveitei a vantagem de jogar com as peças brancas e conduzi a partida à seguinte posição:

– Nesse momento o Maligno cascalhou uma grande risada e clamou: E agora, campeão? Ainda julgas que podes ganhar? Para um jogador de fama seria preferível abandonar! Em sete lances darei o xeque-mate!
– Vamos! Bradei exaltado. Não abandono! Quero ver esse xeque-mate!
– Levamos a partida até o fim. No momento, porém, em que o Diabo deu o lance final, viu-se ele atordoado por um raio vindo dos céus, soltou um pavoroso rugido e desapareceu na fumaça.
– O abalo foi tão grande que rolei meio estonteado pelo chão.
– Quando despertei do susto, as peças do xadrez estavam espalhadas em redor de mim. Ao pé da mesa, pesada de ouro, estava a bolsa escura. Era o prêmio da vitória!
– Havia naquela singular aventura um mistério para mim indecifrável: Por que teria o Diabo abandonado, de repente, a partida já definitivamente ganha por ele?
– Com calma reconstituí, no tabuleiro, lance por lance, a partida jogada. E ao chegar ao golpe final, o caso ficou inteiramente esclarecido: Alá havia inspirado os meus movimentos! No último lance, em que me aplicou o fulminante xeque-mate, o Cheitã formou, diante dos seus olhos, com as oito peças restantes sobre o tabuleiro, a figura perfeita de uma cruz!
– Impossibilitado de suportar a visão daquele símbolo sagrado, o meu infernal adversário retornou ao mundo das trevas, que é o seu lugar!
E com essas palavras o velho campeão dava por finda a narrativa de sua estranha aventura enxadrística.
Os lances finais da partida e a posição derradeira estão aí, para confirmar a história:

Alá seja louvado!

CURIOSIDADE III

A lenda mais conhecida em torno do xadrez fala do hipotético inventor do jogo, que, ao apresentá-lo ao seu rei, viu o entusiasmado monarca prometer-lhe a recompensa que quisesse pela invenção. O súdito fez um pedido insólito: que o rei lhe pagasse em grãos de trigo, 1 pela primeira casa, 2 pela segunda, 4 pela terceira, 8 pela quarta e assim sucessivamente, dobrando a quantidade, até chegar à 64ª casa do tabuleiro. O rei espantou-se com pedido tão modesto e ordenou ao tesoureiro real que pagasse a promessa imediatamente. Não demorou muito para que os matemáticos da corte convencessem o desalentado monarca de que ele fora vítima de um chiste do genial súdito: o número de grãos corresponderia a

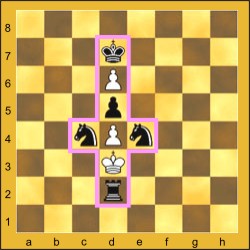
Estudiosos dizem que uma saca de 60kg de trigo tem cerca de 918 mil grãos. Portanto, a recompensa ao inventor ultrapassaria 20 trilhões de sacas. Só para descarregá-las, à razão de uma saca por segundo, seriam demandados mais de 633 mil anos! Aliás, a produção de grãos de trigo no planeta está hoje em 600 milhões de toneladas anuais. Vale dizer que se um rei se dispusesse a pagar tal prêmio nos dias atuais ele teria de arrematar toda a produção mundial de trigo dos próximos dois mil anos!

Conta-se que o jovem inventor aceitou prêmio alternativo: a mão da bela princesa, única filha do rei. E que viveram felizes para sempre.

DOIS PROBLEMAS INSTIGANTES

Extraídos do "Manual de Xadrez" de Idel Becker - 19ª edição

Johann Berger - As brancas jogam e empatam Solução

M. Platov - As brancas jogam e empatam Solução

LISTA CLASSIFICATÓRIA DE ENXADRISTAS ("RANKING")

Entenda como se monta uma lista classificatória de enxadristas ("ranking") e adote o exemplo de tabela montado a seguir, se quiser criar o "ranking" extraoficial dos associados do clube de xadrez de sua cidade.

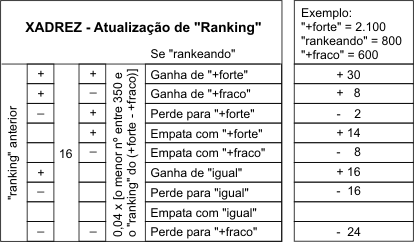
Na prática, use a rotina a seguir, para atualizar o "ranking" dos enxadristas do seu clube, a cada confronto (digite .5 X .5 no caso de empate). Sugere-se que todos comecem com o "ranking" de 350: