CULTURA INÚTIL - Geratriz da dízima periódica

Como estabelecer a geratriz (a fração ordinária que gera uma dízima periódica), por exemplo, do número 74,028379137913791...? A fórmula universal é:

Se não quiser se dar ao trabalho de calcular manualmente, utilize a rotina abaixo:
Int - digite a parte inteira do número, se existir
Frac - digite a parte fracionária não repetitiva, se existir
Rep - digite a parte repetitiva (dízima periódica) só uma vez

CULTURA INÚTIL II - O valor de PI

Sabemos que o valor de PI é um número irracional, que se define pelo limite do produto infinito de

e que resulta em

Se levarmos essa equação a mil termos, mal chegaremos ao valor de PI=3,14 com erro a partir da terceira casa decimal. Ainda que executássemos um milhão de termos

o resultado continuaria desanimador, com o valor de PI=3,14159 e erro a partir da sexta casa decimal. Confira abaixo. Digite um número de termos (de 1 a 1000000) e veja o resultado. Não passe de um milhão, pois o processador dos nossos microcomputadores ainda é muito "lento" para ir além disso. O meu, pelo menos, é:

NÚMEROS SEXAGESIMAIS

Converta um número sexagesimal (graus ou horas) em número decimal. Introduza os valores (graus/horas, minutos e segundos) e tenha o número decimal correspondente:

Converta um número decimal em número sexagesimal (graus ou horas). Introduza o valor decimal e tenha o número sexagesimal correspondente:

DIVISÃO DE A/B COM "N" CASAS DECIMAIS

Divida 'a' por 'b' e obtenha o resultado com o Nº de casas decimais de sua escolha:

O CICLO DA LUA = 29 dias, 12 horas, 44 minutos e 2,78 segundos (29,5305877315 dias)

Cultura Inútil III - 235 "luas" = 19 anos: 235x29,5305877315=6.939,69 e 19x365,24219271=6.939,60

MÍNIMO MÚLTIPLO COMUM (MMC) - MÁXIMO DIVISOR COMUM (MDC)

Para encontrar o MMC de diversos números, decomponha-os em números primos* e depois multiplique os números primos. Exemplificando com os números 2, 4, 5 e 39 [Importante: despreze os nºs primos que não dividam por nada, como o 7 e o 11, no caso]:

2, 4, 5, 39 |  2 
1, 2, 5, 39 |  2     
1, 1, 5, 39 |  3
1, 1, 5, 13 |  5
1, 1, 1, 13 | 13 
1, 1, 1,  1 |

30, 36, 72, 78 |  2 (*) 
15, 18, 36, 39 |  2 
15,  9, 18, 39 |  2
15,  9,  9, 39 |  3 (*)
 5,  3,  3, 13 |  3
 5,  1,  1, 13 |  5
 1,  1,  1, 13 | 13
 1,  1,  1,  1 |

TRIGONOMETRIA

Funções trigonométricas

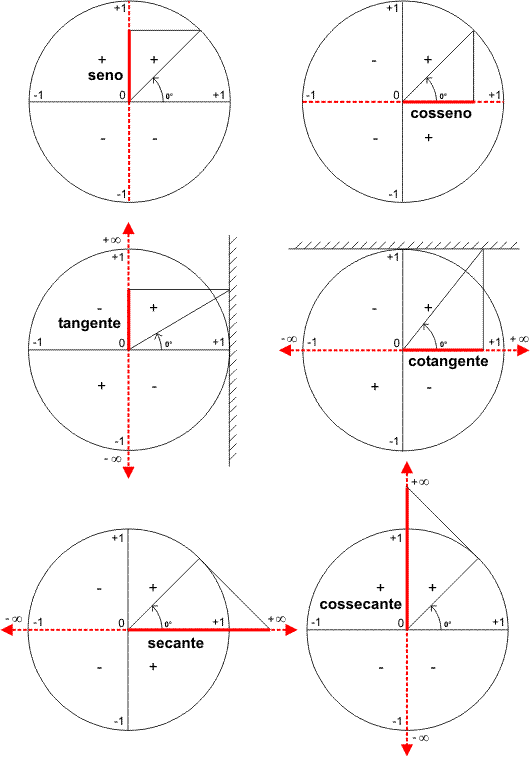
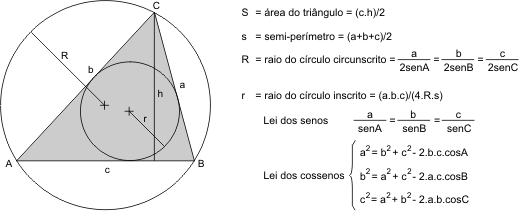
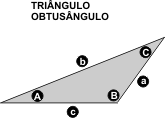
Solução dos triângulos

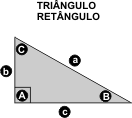
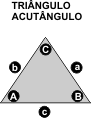
Se não quiser se dar ao trabalho de calcular manualmente, utilize a rotina abaixo, para a resolução de qualquer triângulo (retângulo, acutângulo ou obtusângulo), introduzindo valores decimais. Complete sempre três variáveis, dentre as seis abaixo (A-B-C-a-b-c), sendo que ao menos uma delas há de ser necessariamente a medida de um lado do triângulo (a, b ou c) *

Ângulo A Ângulo B Ângulo C Lado a Lado b Lado c Área(S) ² Alt(h) Raio(R) Raio(r)

Ângulo A Ângulo B Ângulo C Lado a Lado b Lado c Área(S) ² Alt(h) Raio(R) Raio(r)

Ângulo A Ângulo B Ângulo C Lado a Lado b Lado c Área(S) ² Alt(h) Raio(R) Raio(r)

* A informação de três ângulos não define senão a forma do triângulo. Há uma infinidade de triángulos diferentes no tamanho, nada obstante os ângulos sejam idênticos: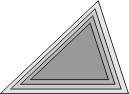

Área de polígonos irregulares

Calcule a área de qualquer polígono irregular, conhecendo-lhe a forma e a medida de ao menos um dos lados. Vejamos o exemplo do polígono abaixo, do qual se conhece a medida do lado superior (10m):

Decomponha o polígono em triângulos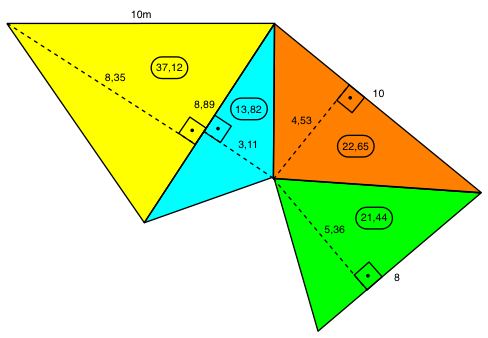
Assinale a altura de cada triângulo (linhas tracejadas)
Aplicando regra de três simples, use a medida conhecida (10m) e calcule base e altura de cada triângulo
Calcule a área de todos os triângulos (base x altura ÷ 2)

Some as áreas de todos os triângulos: 37,12 + 13,82 + 22,65 + 21,44 = 95,03m²

Distância entre dois pontos

Conhecidas as coordenadas geográficas de dois pontos na Terra (Latitude e Longitude), pode-se determinar a distância entre esses dois pontos. Ela equivale ao arco formado entre os pontos a e b, tendo o Centro da Terra como vértice. Cada grau de abertura do ângulo (Â) corresponde a 111,120km, se considerado o raio médio da Terra (r) = 6366,71km (2. π . r / 360). A medida desse arco corresponde a

A Latitude Sul e a Longitude Leste terão valores negativos.

Se não quiser se dar ao trabalho de calcular manualmente, utilize a rotina abaixo, introduzindo valores decimais (não esqueça: valores negativos para Latitudes abaixo da linha do equador e para Longitudes Leste do meridiano de Greenwich):

Latitude ponto a

Longitude ponto a

Latitude ponto b

Longitude ponto b

Distância (km)

---

CULTURA INÚTIL IV - Números Primos

São primos os números inteiros, maiores do que 1, que não têm outro divisor exato senão ele próprio e a unidade. Para comprovar, dividimos o número sucessivamente por 2, 3, 5, 7, 9, 11, 13, 15, 17 etc. até que se alcance uma divisão com resto 0 (e neste caso ele não é um número primo) ou uma divisão com o quociente menor do que o divisor e resto diferente de 0 (e neste caso ele é um número primo).

Utilize a rotina abaixo, introduzindo um número inteiro, e veja se ele é número primo. Se a resposta for negativa, aparecerá o terceiro divisor exato para comprová-lo: