|
DIRECIONAMENTO DE ANTENA PARABÓLICA UNIVERSAL

OS ÂNGULOS "X" e "Y" Introduza a Latitude de sua cidade, com frações decimais. Exemplo: 27.8 (27º48') que produz os resultados X=4.072 e Y=28.3844. O sinal "+" ou "-" é indiferente, seja para latitudes acima ou abaixo da linha do equador. Os resultados "X" e "Y" serão também em graus decimais. Os valores de "a" e "b" serão úteis mais tarde, se você quiser construir o inclinómetro descrito mais abaixo. 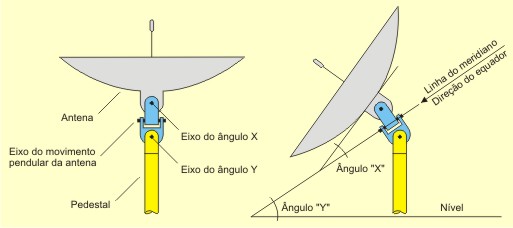
OS LIMITES DE FUNCIONAMENTO
O NORTE VERDADEIRO Use a rotina abaixo para calcular o "trânsito" do Sol em sua cidade. Introduza a Longitude de sua cidade (Graus com sinal "-" se você estiver a Leste de Greenwich), ou selecione na lista prévia. Se for o caso, altere o Fuso Horário (sinal "-" se você estiver a Leste de Greenwich) e mude a data. Atenção: Se a sua cidade não estiver na lista é imprescindível selecionar "A sua cidade →" e sobreescrever os dados que porventura tiverem sido registrados antes.
OS AJUSTES - O INCLINÓMETRO 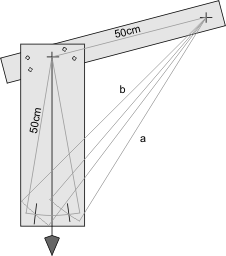
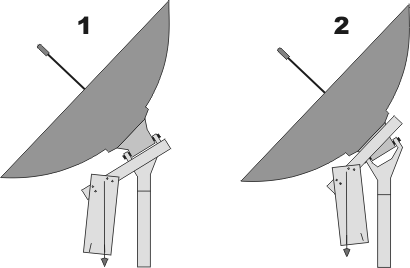
O MOVIMENTO PENDULAR DA ANTENA Se os ângulos e o Norte da antena estiverem corretos, esse movimento pendular rastreará todos os satélites geoestacionários do hemisfério, restando saber para quais satélites se quer apontá-la e em que "altura" eles se encontram no céu, mediante consulta às revistas ou aos "sites" especializados. Se você preferir montar um semidisco graduado, solidário ao eixo da antena, para facilitar o direcionamento, tenha em conta que a antena na posição horizontal (nivelada) aponta exatamente para os graus de Longitude da sua cidade. Assim, se sua cidade está a 51°W, por exemplo, a marca central do semidisco corresponderá a 51. Se o semidisco estiver dividido em 180 graus, para o Oeste você terá 52, 53, 54, 55... 141°W e para o Leste você terá 50, 49, 48, 47°W... 39°E. 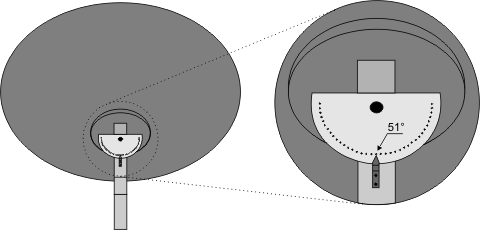
AS FÓRMULAS MATEMÁTICAS
APÊNDICE
Assumimos que todos os satélites geoestacionários orbitam a Terra à altura de 35.786km, exatamente acima da linha do equador. E que, como eles acompanham o giro da Terra, parecem estar parados no céu. A órbita deles forma um anel imaginário ao redor da Terra, denominado "Anel de Clarke". Assumimos, também, que o círculo do equador tem o raio de 6.378,16km.
Assim, para apontarmos a antena para o Anel de Clarke, nós a direcionamos para o zênite (ponto
mais alto do céu) e a tombamos na direção Norte (se estamos no hemisfério Sul) ou na direção Sul (se estamos no
hemisfério Norte), em um ângulo determinado pela latitude da nossa cidade. Se a nossa cidade se situa na latitude zero (na linha do equador), a antena direcionada para o zênite já aponta para o Anel de Clarke.
Depois é só direcioná-la para o satélite desejado, sabendo sua longitude. Para tanto será necessário estabelecer um eixo que possibilite criar um movimento pendular da antena.
Se estamos na linha do equador (latitude zero), tudo fica mais fácil: o eixo estará paralelo ao eixo da Terra e do Anel de Clarke e bastará realizar o movimento pendular da antena, para Leste ou para Oeste, procurando o satélite desejado, em sua longitude.
Se estamos no Polo Norte ou no Polo Sul (latitude 90º), a equação também é fácil: o eixo estará perpendicular ao eixo da Terra e do Anel de Clarke e bastará tombar a antena num ângulo de 8,6019º e girar o pedestal à procura da longitude do satélite desejado.
Por que 8,6019º? Porque é a solução do triângulo-retângulo abaixo ilustrado (resolva-o utilizando a rotina da minha página "Soluções Matemáticas" - os valores conhecidos estão em vermelho):
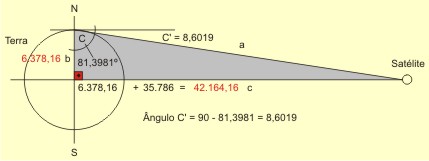 O desenho acima é teórico. Já dissemos que uma antena situada num dos polos, no nível do chão, não "enxergará" os satélites geoestacionários, por causa da curvatura da Terra. Só os "enxergaria" se estivesse sobre uma torre com a altura impraticável de 74,2507km. No nível do chão, a maior latitude em que uma antena "enxerga" os satélites está em 81,2995º. Por que 74,2507km e 81,2995º? Porque é a solução dos dois triângulos-retângulos abaixo ilustrados (resolva-os utilizando a rotina da minha página "Soluçães Matemáticas" – os valores conhecidos estão em vermelho), que têm como um dos catetos uma linha que parte dos satélites e tangencia a Terra:  Todavia, se estamos numa latitude intermediária, maior do que zero e menor do que 90º, o cálculo se torna mais complicado. É preciso determinar o ângulo do eixo do rastreamento pendular e é preciso compensar a excentricidade da curva imaginária traçada pela antena no céu, uma vez que ela estará fora do eixo da Terra e do eixo do Anel de Clarke. Trabalhemos com a latitude hipotética de 27,8º S (27º48') e vejamos no desenho que isso significaria tombar uma antena apontada para o zênite 32,4564º em direção ao Norte. Use minha página "Soluçães Matemáticas" para resolver os triângulos a seguir. Os valores previamente conhecidos estão apresentados em vermelho. Resolva os dois triângulos-retângulos abaixo: 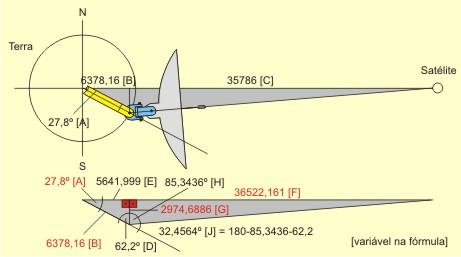 O ângulo total de tombamento da antena (32,4564º) a aponta para o plano do Anel de Clarke (o plano do equador). Todavia, o movimento pendular da antena a afastaria do plano do equador, uma vez que o eixo do movimento pendular não está paralelo ao eixo da Terra: 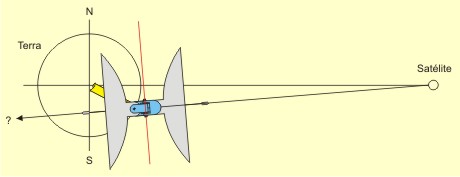 Faz-se necessário verticalizar o eixo do movimento pendular da antena, para que ele fique paralelo ao eixo da Terra. O eixo deverá ser destombado 4,6564º (32,4564 - 27,8) e, para compensar, a antena deverá ser tombada idênticos 4,6564º, ficando portanto o ângulo "X" com 4,6564º e o ângulo "Y" com 27,8º: 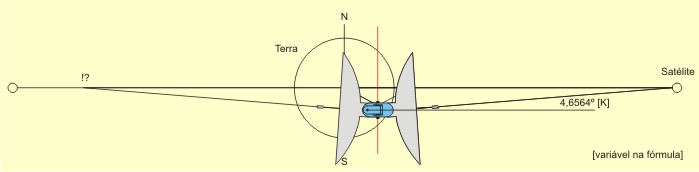 Acontece que, conquanto agora a antena focalize o Anel de Clarke, se apontada para o zênite, ela não o alcançaria quando apontada para o horizonte. Veja no 1º desenho abaixo que o Anel de Clarke, no horizonte, está mais longe do que no zênite, no ponto de vista da antena. Faz-se necessário corrigir isso, diminuindo o tombamento da antena, pelos 0,5844º encontrados no 2º desenho, para que ela alcance o Anel de Clarke, quando apontada para o horizonte. Ao mesmo tempo, faz-se necessário aumentar o tombamento do eixo do movimento pendular da antena, pelos mesmos 0,5844º, para reconduzi-la ao foco do Anel, quando apontada para o zênite. O que conduz o ângulo "X" a 4,072º (4,6564 - 0,5844) e o ângulo "Y" a 28,3844 (27,8 + 0,5844):  Depois é só direcionar a antena para o satélite desejado, sabendo sua longitude. A antena posicionada na linha do equador rastreará os satélites do hemisfério mediante movimento pendular: 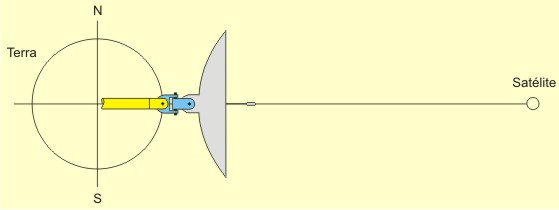 A antena posicionada em um dos polos rastrearia os satélites do mundo inteiro (se a curvatura da Terra não impedisse a visualização) mediante o giro do pedestal no eixo Norte-Sul: 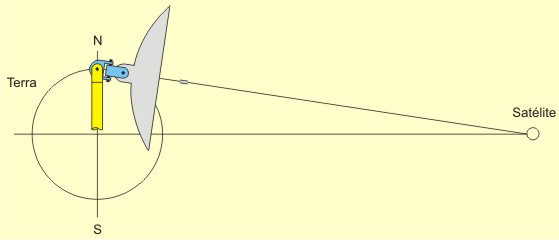 A antena posicionada em qualquer outra latitude rastreará os satélites do hemisfério mediante movimento pendular: 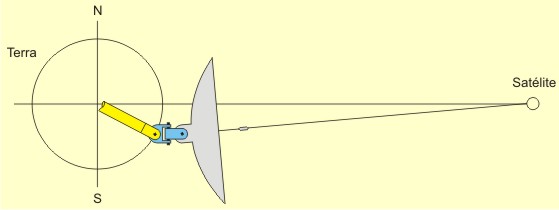 Veja o interessante vídeo feito para confirmar que as fórmulas acima estão corretas e conduzem ao perfeito rastreamento da antena em cima do Anel de Clarke. O filme foi feito sob critérios técnicos, com base em desenho tridimensional no AutoCad, e traz uma câmara fotográfica que acompanha a trajetória apontada pela antena: Se quiser saber mais a respeito da recepção de sinais de satélites, veja uma profusão de informaçães importantes, na página em inglês Satellite Signals, de Eric Johnston.
|
© 21/09/2002 Atualizada em 17/03/2025